[勉強ノート] 「拡散モデル データ生成技術の数理」 3.1-3.5のVE-SDE部分について
先日紹介した「拡散モデル データ生成技術の数理」をちゃんと理解するために数式を改めて追ったり、説明されているアルゴリズムを実装をしたりしたものをまとめた記事の第4弾です。今回は3章の分散発散型確率微分方程式 (VE-SDE)の部分のコードを書いたのでVE-SDEの式の簡単な説明とコードの解説記事になります。
今回の記事はスコアベースモデル (SBM)はすでに理解している前提で説明していきます。もしスコアベースモデルがよくわからないという方はこちらに簡単な解説を書いたので参考にしてください。
今回のコードは以下のところにあげてありますので、コード全体を見たい方はこちらをご覧ください。
https://github.com/shu65/diffusion-model-book/blob/main/diffusion_model_book_3_VE_SDE.ipynb
目次
分散発散型確率微分方程式(VE-SDE)とは?
この本の3章の前半部分で、2章で紹介しているスコアベースモデル (SBM)とデノイジング拡散確率モデル (DDPM) を確率微分方程式 (SDE) とみなすことができるという説明をしています。このうち、SBMのほうをSDE表現してでてくるものが分散発散型確率微分方程式 (VE-SDE)です。
確率微分方程式(SDE)
確率微分方程式(SDE; Stochastic Differential Equations)は次の式で与えられます。
$$ \begin{align} \text{d}\boldsymbol{x} = \boldsymbol{f}(\boldsymbol{x}, t)\text{d}t + \boldsymbol{G}(\boldsymbol{x}, t)\text{d}\boldsymbol{w} \tag{3.1} \end{align} $$
この式において\(\text{d}\boldsymbol{x} \)は\(\boldsymbol{x}\)の変化量です。この変化量は決定的に変化量である\(\boldsymbol{f}(\boldsymbol{x}, t)\text{d}t\)とランダムに変化する量である\(\boldsymbol{G}(\boldsymbol{x}, t)\text{d}\boldsymbol{w}\)の和で構成されています。
ここで、\(\boldsymbol{w}\)は標準ウィーナー過程またはブラウン運動ともよばれ、\(\text{d}\boldsymbol{w}\)は微小時間間隔\(\tau\)において平均が0、分散が\(\tau\)の正規分布とみなすことができます。
この確率微分方程式において\(\boldsymbol{f}(\cdot, t)\)はドリフト係数、\(\boldsymbol{G}(\cdot, t)\)は拡散係数と呼びます。
ただし、一般に拡散モデルで扱う確率微分方程式以下のようにドリフト係数が時間のみに依存する関数\(\boldsymbol{f}(t)\)と入力\(\boldsymbol{x}\)の積、拡散係数は時間のみに依存してスカラ値を出力する\(g(t)\)を使った確率微分方程式が利用されます。
$$ \begin{align} \text{d}\boldsymbol{x} = f(t)\boldsymbol{x}\text{d}t +g(t)\text{d}\boldsymbol{w} \tag{3.2} \end{align} $$
スコアベースモデルの拡散過程をSDEで表現する
スコアベースモデル(SBM)の拡散過程は以下のようになっていました。
$$ \begin{align} q(\boldsymbol{x}_i | \boldsymbol{x}) = \mathcal{N}(\boldsymbol{x}, \sigma_i^2\boldsymbol{I}) \tag{3.3} \end{align} $$
ここで\(i = 0,…, N\)です。この場合の拡散過程の1ステップは次のようになります。
$$ \begin{align} q(\boldsymbol{x}_i | \boldsymbol{x}_{i-1}) = \mathcal{N}(\boldsymbol{x}_i;\boldsymbol{x}_{i-1}, (\sigma_i^2 – \sigma_{i-1}^2)\boldsymbol{I}) \tag{3.4}
\end{align} $$
式(3.3), (3.4)は2章のほうで説明されています。この拡散過程の1ステップは変数変換を使うと以下のようになります。
$$ \begin{align}
\boldsymbol{x}_i &= \boldsymbol{x}_{i-1} + \sqrt{\sigma_i^2 – \sigma_{i-1}^2}\boldsymbol{z}_{i-1} \tag{3.5} \\
\boldsymbol{z}_{i-1} &\sim \mathcal{N}(0, \boldsymbol{I}) \tag{3.6}
\end{align} $$
ここで簡略化のために\(\sigma_0 = 0\) として考えます。
ここから\(N \rightarrow \infty\) とした極限を考えていきます。この時、\(i\)の代わりに\(t\)を用いて、\({\boldsymbol{x}_i}_{i=1}^N\)を連続的な確率過程\({\boldsymbol{x}_t}_{t=0}^1\)とし、\(\sigma_i\)を関数\(\sigma(t)\)、\(\boldsymbol{z}_{i}\)は\(\boldsymbol{z}(t)\)とします。
また、\(\Delta t=1/N\)とし、\(t \in \left\{0, \frac{1}{N},…, \frac{N-1}{N} \right\}\)とします。
この時式(3.5)の式は以下のようになります。
$$ \begin{align} \boldsymbol{x}(t + \Delta t) = \boldsymbol{x}(t) + \sqrt{\sigma(t + \Delta t)^2 – \sigma(t)^2}\boldsymbol{z}_{i-1} \tag{3.7} \end{align} $$
ここで\(\sigma(t + \Delta t)^2 – \sigma(t)^2\)の部分で1次近似を利用して式変形します。1次近似は以下の近似を指します。
$$ \begin{align} f(x + \Delta x) \approx \frac{\text{d}f(x)}{\text{d}x} \Delta x + f(x) \tag{3.8} \end{align} $$
この1次近似の式において\(f(x)\)の部分を\(\sigma(t)^2\)として置き換えると以下のようになります。
$$ \begin{align} \sigma(t + \Delta t)^2 \approx \frac{\text{d}[\sigma(t)^2]}{\text{d}t} \Delta t + \sigma(t)^2 \tag{3.9} \end{align} $$
この式の両辺を\(\sigma(t)^2\)で引くと以下のようになります。
$$ \begin{align} \sigma(t + \Delta t)^2 – \sigma(t)^2 \approx \frac{\text{d}[\sigma(t)^2]}{\text{d}t} \Delta t \tag{3.10} \end{align} $$
この式(3.10)を式(3.7)に代入すると以下のようになります。
$$ \begin{align} \boldsymbol{x}(t + \Delta t) = \boldsymbol{x}(t) + \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t} \Delta t}\boldsymbol{z}(t) \tag{3.11} \end{align} $$
このあとの説明のために以下のように少し式変形をします。
$$ \begin{align}
\boldsymbol{x}(t + \Delta t) &= \boldsymbol{x}(t) + \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t} \Delta t}\boldsymbol{z}(t) \\
\boldsymbol{x}(t + \Delta t) – \boldsymbol{x}(t) &= \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t} \Delta t}\boldsymbol{z}(t) \\
\boldsymbol{x}(t + \Delta t) – \boldsymbol{x}(t) &= \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t}} \left(\sqrt{\Delta t}\boldsymbol{z}(t) \right) \tag{3.12}
\end{align} $$
さて、ここから\(\Delta t \to 0\) にしたときのことを考えます。式(3.12)の左辺のほうは以下のようになります。
$$ \begin{align}
\lim_{\Delta t \to 0} \boldsymbol{x}(t + \Delta t) – \boldsymbol{x}(t) = \text{d}\boldsymbol{x} \tag{3.13}
\end{align} $$
問題は右辺の\(\sqrt{\Delta t}\boldsymbol{z}(t) \)の部分です。これは結果的には以下のようになります。
$$ \begin{align}
\lim_{\Delta t \to 0} \sqrt{\Delta t}\boldsymbol{z}(t) = \text{d}\boldsymbol{w} \tag{3.14}
\end{align} $$
この部分ですが本も元論文[3] のほうにもこの式変形のところで言及がないのでわかりにくいので少し説明します。
まず、そもそも\(\text{d}\boldsymbol{w}\)は何であったか?ですが、これは最初に説明した通り標準ウィーナー過程またはブラウン運動ともよばれ、\(\text{d}\boldsymbol{w}\)は微小時間間隔\(\tau\)において平均が0、分散が\(\tau\)の正規分布とみなすことができます。このことから以下のように表すことができます。
$$ \begin{align}
\text{d}\boldsymbol{w} \sim \mathcal{N}(0, \tau \boldsymbol{I}) \tag{3.15}
\end{align} $$
ここで\(\boldsymbol{z}(t)\)は
$$ \begin{align}
\boldsymbol{z}(t) \sim \mathcal{N}(0, \boldsymbol{I}) \tag{3.16} \\
\end{align} $$
なので、\(\text{d}\boldsymbol{w}\)は以下のようになります。
$$ \begin{align}
\text{d}\boldsymbol{w} = \sqrt{\tau} \boldsymbol{z}(t) \tag{3.17}
\end{align} $$
\(\tau\)が微小時間間隔なので式(3.14)と式(3.17)を見比べるとなんとなく式(3.14)が成り立ちそうだなぁと思います。ただ、極限を素直に考えると以下のようになるのでは?とずっと思ってました。
$$ \begin{align}
\lim_{\Delta t \to 0} \sqrt{\Delta t}\boldsymbol{z}(t) = 0
\end{align} $$
この部分、私は気になってしょうがなかったので、少し調べました。結論からいうとこの部分の式変形に関してはウィーナー過程の条件から導出できそうだということがわかりました。詳しくは以下のサイトが分かりやすかったので、詳しく知りたい方はご覧ください。
http://takashiyoshino.random-walk.org/memo/keikaku_ensyu/node4.html
ここでは簡単に説明します。まずウィーナー過程 \(\boldsymbol{w}(t)\)を考えます。ウィナー過程の条件より以下が成り立ちます。
$$ \begin{align}
\boldsymbol{w}(t + \Delta t) – \boldsymbol{w}(t) \sim \mathcal{N}(0, \Delta t \boldsymbol{I}) \tag{3.18}
\end{align} $$
ここで式(3.18)を右辺を見ると平均0、分散\(\Delta t\)の正規分布です。このため、式(3.18)は左辺は以下のように表すこともできます。
$$ \begin{align}
\boldsymbol{w}(t + \Delta t) – \boldsymbol{w}(t) = \sqrt{\Delta t}\boldsymbol{z}(t) \tag{3.19} \\
\end{align} $$
この式(3.19)の右辺は式(3.14)の左辺の\(\lim_{\Delta t \to 0}\)の中と同じになります。また式(3.19)の左辺は\(\Delta t \to 0\)のとき以下のようになります。
$$ \begin{align}
\lim_{\Delta t \to 0} \left( \boldsymbol{w}(t + \Delta t) – \boldsymbol{w}(t) \right) &= \text{d}\boldsymbol{w} \tag{3.20}
\end{align} $$
よって式(3.14)は式(3.19)と(3.20)を使うと以下のようになります。
$$ \begin{align}
\lim_{\Delta t \to 0} \sqrt{\Delta t}\boldsymbol{z}(t) &= \lim_{\Delta t \to 0} \left( \boldsymbol{w}(t + \Delta t) – \boldsymbol{w}(t) \right) \\
&= \text{d}\boldsymbol{w} \tag{3.21}
\end{align} $$
この式変形なら個人的には納得できました。よって最終的に式(3.12)で\(\Delta t \to 0\) を考えると式(3.13)と式(3.21)より以下のようになります。
$$ \begin{align}
\text{d}\boldsymbol{x} &= \lim_{\Delta t \to 0} \boldsymbol{x}(t + \Delta t) – \boldsymbol{x}(t) \\
&= \lim_{\Delta t \to 0} \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t}} \left(\sqrt{\Delta t}\boldsymbol{z}(t) \right) \\
&= \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t}} \boldsymbol{w}(t) \tag{3.22}
\end{align} $$
この式(3.22)を見るとドリフト係数\(f(t)\) と拡散係数\(g(t)\)が以下のようなSDEであることが分かります。
$$ \begin{align*}
f(t) &= 0 \tag{3.23} \\
g(t) &= \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t}} \tag{3.24} \\
\end{align*} $$
これでSBMをSDEで表現することができました。このSBMの式から導出したSDEを分散発散型確率微分方程式 (VE-SDE)と呼びます。
VE-SDEの学習
VE-SDEの各時刻\(t\)のスコアを学習するあために、次の条件付き確率(拡散カーネル)を知る必要があります。
$$ \begin{align*}
p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) \tag{3.25}
\end{align*} $$
ここで\(p_{0t}\)は\(\boldsymbol{x}(0)\)を条件付けしたときの\(\boldsymbol{x}(t)\)の確率を表しています。
ここでSDEが以下の形として考えていきます。
$$ \begin{align} \text{d}\boldsymbol{x} = f(t)\boldsymbol{x}\text{d}t + g(t)\text{d}\boldsymbol{w} \end{align} \tag{3.26}$$
この場合、式(3.26)の条件付き確率は以下のような正規分布で表すことができます[1, 2]。
$$ \begin{align}
p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) =& \mathcal{N}(s(t)\boldsymbol{x}(0), s(t)^2\sigma^{\prime}(t)^2\boldsymbol{I}) \tag{3.27} \\
s(t) =& \text{exp}\left(\int_0^tf(\xi)\text{d}\xi\right) \tag{3.28} \\
\sigma^{\prime}(t) =& \sqrt{\int_0^t \frac{g(\xi)^2}{s(\xi)^2}\text{d}\xi} \tag{3.29} \\
\end{align} $$
本のほうでは式(3.27)と式(3.29) の\(\sigma^{\prime}(t)\)の部分は\(\sigma(t)\)という表記になっています。ただ、VE-SDEのほうにも\(\sigma(t)\)があって区別ができないので、この記事では式(3.27)と(3.29)に登場する\(\sigma(t)\)を\(\sigma^{\prime}(t)\)として説明していきます。
VE-SDEの場合はこの式を使うと簡単に\(p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0))\)の形がわかるので、以下に示していきます。
まず、\(s(t)\)の部分ですが、VE-SDEの場合、式(3.23)から以下のようになります。
$$ \begin{align}
s(t) &= \text{exp}\left(\int_0^tf(\xi)\text{d}\xi\right) \\
&= \text{exp}\left(\int_0^t 0 \text{d}\xi\right) \\
&= \text{exp}\left(0 \right) \\
&= 1 \tag{3.30} \\
\end{align} $$
次に\(\sigma^{\prime}(t)\)に関してです。まず式(3.26)を使って式変形します。
$$ \begin{align}
\sigma^{\prime}(t) &= \sqrt{\int_0^t \frac{g(\xi)^2}{s(\xi)^2}\text{d}\xi} \\
&= \sqrt{\int_0^t \frac{g(\xi)^2}{1^2}\text{d}\xi} \\
&= \sqrt{\int_0^t g(\xi)^2\text{d}\xi} \tag{3.31}
\end{align} $$
ここでVE-SDEの\(g(t)\)は式(3.24)で分かっているのでこれを利用してさらに式変形します。
$$ \begin{align}
\sigma^{\prime}(t) &= \sqrt{\int_0^t g(\xi)^2\text{d}\xi} \\
&= \sqrt{\int_0^t \left( \sqrt{\frac{\text{d}[\sigma(\xi)^2]}{\text{d}\xi}} \right)^2\text{d}\xi } \\
&= \sqrt{\int_0^t \frac{\text{d}[\sigma(\xi)^2]}{\text{d}\xi} \text{d}\xi } \\
&= \sqrt{\sigma(t)^2 – \sigma(0)^2} \tag{3.32}
\end{align} $$
式変形した式(3.30)、(3.32)を式(3.27)に代入すると最終的には以下のようになります。
$$ \begin{align}
p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) &= \mathcal{N}(s(t)\boldsymbol{x}(0), s(t)^2\sigma^{\prime}(t)^2\boldsymbol{I}) \\
&= \mathcal{N}(\boldsymbol{x}(0), \left[\sigma(t)^2 – \sigma(0)^2\right]\boldsymbol{I}) \tag{3.33}
\end{align} $$
これによりVE-SDEの拡散過程の条件付き確率の式がわかりました。
本の説明では\(\sigma(t)\)が具体的にどのような式を使うのかまでは示してないため、式変形はここまでになっています。
一方、このブログではコードに落とすところまでをやるため、ここからさらに式変形していきます。ここから元論文の[3]を参考にして式変形していきます。
[3]の論文で使われている\(\sigma(t)\)と同じものを用いて説明していきます。[3]では以下のものが使われています。
$$ \begin{align}
\sigma(t) &= \sigma_{min}\left( \frac{\sigma_{max}}{\sigma_{min}} \right)^t, & \ t &\in (0, 1] \\
\sigma(0) &= 0, & \ t &= 0 \\
\tag{3.34}
\end{align} $$
ここで\(\sigma_{min}\)と\(\sigma_{max}\)はハイパーパラメータです。
これを使って式(3.24)の\(g(t)\)と式(3.33)の条件付き確率の式変形をしていきます。
まず、式(3.24)の\(g(t)\)に関してです。
$$ \begin{align*}
g(t) &= \sqrt{\frac{\text{d}[\sigma(t)^2]}{\text{d}t}} \\
&= \sqrt{\frac{\text{d}}{\text{d}t} \left( \sigma_{min}\left( \frac{\sigma_{max}}{\sigma_{min}} \right)^t \right)^2} \\
&= \sqrt{\frac{\text{d}}{\text{d}t} \sigma_{min}^2\left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} } \\
&= \sqrt{\sigma_{min}^2 \frac{\text{d}}{\text{d}t} \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} } \tag{3.35}
\end{align*} $$
ここで\( \frac{\text{d}}{\text{d}t} \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} \)の部分に注目します。以下のような指数関数の微分公式を利用します。
$$ \begin{align*}
\frac{\text{d}}{\text{d}x} a^x = a^x \log a \tag{3.36}
\end{align*} $$
(参考:https://manabitimes.jp/math/1112)
この公式を利用すると以下のようになります。
$$ \begin{align*}
\frac{\text{d}}{\text{d}t} \left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} &= \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} \log \left(\frac{\sigma_{max}}{\sigma_{min}} \right)^2
\tag{3.37}
\end{align*} $$
この式(3.37)を式(3.35)に代入して式変形していくと以下のようになります。
$$ \begin{align*}
g(t) &= \sqrt{\sigma_{min}^2 \frac{\text{d}}{\text{d}t} \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} } \\
&= \sqrt{\sigma_{min}^2 \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} \log \left(\frac{\sigma_{max}}{\sigma_{min}} \right)^2 } \\
&= \sigma_{min} \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{t} \sqrt{\log \left(\frac{\sigma_{max}}{\sigma_{min}} \right)^2 } \\
&= \sigma_{min} \left( \frac{\sigma_{max}}{\sigma_{min}} \right)^{t} \sqrt{2 \log \left(\frac{\sigma_{max}}{\sigma_{min}} \right)} \tag{3.38}
\end{align*} $$
次に式(3.33)の条件付き確率のほうを式変形していきます。この式には分散のほうにだけ\(\sigma(t)\)が登場するので、この部分だけ注目します。この分散に式(3.34)の\(\sigma(t)\)を代入して式変形していくと以下のようになります。
$$ \begin{align}
\sigma(t)^2 – \sigma(0)^2 &= \left[\sigma_{min}\left( \frac{\sigma_{max}}{\sigma_{min}} \right)^t \right]^2 – 0^2 \\
&= \sigma_{min}^2\left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t} \\ \tag{3.39}
\end{align} $$
よって式(3.33)の条件付き確率は以下のようになります。
$$ \begin{align}
p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) &= \mathcal{N}(\boldsymbol{x}(0), \left[\sigma(t)^2 – \sigma(0)^2\right]\boldsymbol{I}) \\
&= \mathcal{N}\left(\boldsymbol{x}(0), \sigma_{min}^2\left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t}\boldsymbol{I}\right) \tag{3.40}
\end{align} $$
これらを用いてデノイジングスコアマッチングをロス関数としてスコア関数\(s_{\theta}\)を学習します。VE-SDEの場合のデノイジングスコアマッチングの関数はSBMのときと同じ形になります。具体的には以下のようになります。(変数はVE-SDEに合わせています。)
$$ \begin{align}
L(\theta) :=&
E_t \left[ \lambda(t) E_{\boldsymbol{x}(0) \sim p_{data}(\boldsymbol{x}),\boldsymbol{x}(t) \sim p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0))} \left\{ \right. \right. \\
& \quad \left. \left. \left| \nabla_{\boldsymbol{x}(t)} \log p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) – s_{\theta}(\boldsymbol{x}(t), t) \right|^2 \right\} \right] \tag{3.41}
\end{align} $$
ここで、\(\lambda(t)\)は各\(t\)における重みづけです。
これを実装するために、SBMのときと同じようにスコア \( \nabla_{\boldsymbol{x}(t)} \log p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) \)の部分を式変形します。これはSBMのときと同じなので本の2章と以前私が書いたSBMの解説の記事をご覧ください。
結果として以下のようになります。
$$ \begin{align}
\nabla_{\boldsymbol{x}(t)} \log p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) &= \frac{-\epsilon}{\sigma_{min}^2\left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t}} \tag{3.42} \\
\epsilon &\sim \mathcal{N}\left(0, \sigma_{min}^2\left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t}\boldsymbol{I}\right) \tag{3.43}
\end{align} $$
式(3.41)を式(3.42)、(3.43)を使って変形すると以下のようになります。(式が長すぎるので\(\boldsymbol{x}(0), \boldsymbol{x}(t), \epsilon\)の分布を省略してます。)
$$ \begin{align}
L(\theta) :=&
E_t \left[ \lambda(t) E_{\boldsymbol{x}(0),\boldsymbol{x}(t)} \left\{ \left| \nabla_{\boldsymbol{x}(t)} \log p_{0t}(\boldsymbol{x}(t)|\boldsymbol{x}(0)) – s_{\theta}(\boldsymbol{x}(t), t) \right|^2 \right\} \right] \\
=& E_t \left[ \lambda(t) E_{\boldsymbol{x}(0),\epsilon} \left\{ \left| \frac{-\epsilon}{\sigma_{min}^2\left(\frac{\sigma_{max}}{\sigma_{min}} \right)^{2t}} – s_{\theta}(\boldsymbol{x}(t), t) \right|^2 \right\} \right] \tag{3.44}
\end{align} $$
これをPyTorchを使ってコードにすると以下のようになります。
def sigma(t, sigma_min=sigma_min, sigma_max=sigma_max):
return sigma_min * (sigma_max / sigma_min) ** t
def ve_sde_marginal_prob_statistics(x, t, sigma_min, sigma_max):
mean = x
std = sigma(t=t, sigma_min=sigma_min, sigma_max=sigma_max)
return mean, std
def ve_sde_drift(t, sigma_min, sigma_max):
drift = torch.zeros_like(t)
return drift
def ve_sde_diffusion(t, sigma_min, sigma_max):
std = sigma(t=t, sigma_min=sigma_min, sigma_max=sigma_max)
diffusion = std * torch.sqrt(2 * (torch.log(sigma_max) - torch.log(sigma_min))) # (30)
return diffusion
def dsm_loss(score_model, samples, sigma_min, sigma_max):
eps = 1.0e-8
t = torch.distributions.uniform.Uniform(torch.tensor([eps], device=samples.device), torch.tensor([1], device=samples.device)).sample([samples.shape[0]])
z = torch.randn_like(samples)
mean, std = ve_sde_marginal_prob_statistics(x=samples, t=t, sigma_min=sigma_min, sigma_max=sigma_max)
noise = z * std
perturbed_samples = mean + z * std
scores = score_model(perturbed_samples, t)
target = - 1 / (std ** 2) * noise
target = target.view(target.shape[0], -1)
scores = scores.view(scores.shape[0], -1)
g = ve_sde_diffusion(t=t, sigma_min=sigma_min, sigma_max=sigma_max)
lmd = g ** 2
loss = torch.sqrt(((scores - target) ** 2).sum(dim=-1)) * lmd
return loss.mean()ここで本によると\(\lambda(t)=g(t)^2\)のときにスコアマッチングの目的関数は負の対数尤度の上限となっていることが証明できるそうです。このため、上記のコードでは\(\lambda(t)=g(t)^2\)を利用しています。
VE-SDEのサンプリング
VE-SDEのサンプリングをするためには拡散過程を逆にたどる逆算過程を知る必要があります。
拡散過程のSDEは式(3.1)で与えらえるとするとこの逆算過程は以下のようになります。
$$ \begin{align} \text{d}\boldsymbol{x} =& \left\{f(\boldsymbol{x}, t) – \nabla \left[ \boldsymbol{G}(\boldsymbol{x}, t) \boldsymbol{G}(\boldsymbol{x}, t)^\text{T} \right] \right. \\
& \quad \left. – \left[ \boldsymbol{G}(\boldsymbol{x}, t) \boldsymbol{G}(\boldsymbol{x}, t)^\text{T} \right] \nabla_{\boldsymbol{x}} \log p_t(\boldsymbol{x})\right\} \text{d}t \\
& \quad+ \boldsymbol{G}(\boldsymbol{x}, t)\text{d}\bar{\boldsymbol{w}} \tag{3.45} \end{align} $$
ただし、\(\text{d}\bar{\boldsymbol{w}}\)は時刻Tから0まで客向きに辿ったときの標準ウィーナー過程です。
ただし、一般的に拡散もモデルで使われる確率微分方程式は式(3.2)の形だそうです。このため式(3.2)で使われている\(f(t), g(t)\)で式(3.45)を書き直すと以下のようになります。
$$ \begin{align} \text{d}\boldsymbol{x} =& \left[f(t) – g(t)^2\nabla \log p_t(\boldsymbol{x})\right] \text{d}t + g(t)\text{d}\bar{\boldsymbol{w}} \tag{3.46} \end{align} $$
式(3.45)と式(3.46)の式変形の説明も本当はやろうと思ったのですが、かなり長い式変形になるのと、本の付録のほうに詳しい説明があるのでこの記事では省略します。
この式(3.46)に基づいて拡散モデルのサンプリングをする方法としてオイラー・丸山先生によるサンプリングが本で紹介されています。疑似コードは以下の通りです。(「拡散モデル データ生成技術の数理」Algorithm 3.1の引用)
- \(\boldsymbol{x} \sim \mathcal{N}(0, \boldsymbol{I})\))
- for \(i=T,…,1\) do
- \(\quad \boldsymbol{z}_i \sim \mathcal{N}(0, \boldsymbol{I})\)
- \(\quad \boldsymbol{x} := \boldsymbol{x} – \left[f(t_i) – g(t_i)^2 s_{\theta}(\boldsymbol{x}, t_i)\right] \Delta t_i + g(t)\sqrt{|\Delta t_i|} \boldsymbol{z}_i \)
- end for
- return \(\boldsymbol{x}\)
これをPyTorchで実装すると以下のようになります。
def euler_maruyama_sample(n_samples, score_model, device=device, n=1000):
with torch.no_grad():
x = torch.randn(n_samples, 2, device=device)
dt = torch.tensor(1.0 / n, device=x.device)
for t in range(n, 0, -1):
t_tensor = torch.full((n_samples, 1), t/n, device=device)
z = torch.randn(n_samples, 2)
f = ve_sde_drift(t_tensor, score_model.sigma_min, score_model.sigma_max)
g = ve_sde_diffusion(t_tensor, score_model.sigma_min, score_model.sigma_max)
g2 = g ** 2
score = score_model(x, t_tensor)
x = x - (f*x - g2 * score) * dt + g * torch.sqrt(dt) * z
return xコードの実行例
ここでは先ほど紹介したロス関数とサンプリング関数を利用して実際にVE-SDEでスコア関数のパラメータを学習し、サンプリングした例を示します。
参考例として入力となる\(\boldsymbol{x}\)のサンプリングする分布の確率密度関数は以下のように平均が違うガウス分布二つの混合分布とし、サンプリングしたデータを正規化して使用します。
n_samples = int(1e6)
sigma = 0.01
dist0 = torch.distributions.MultivariateNormal(torch.tensor([-2, -2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples0 = dist0.sample(torch.Size([n_samples//2]))
dist1 = torch.distributions.MultivariateNormal(torch.tensor([2, 2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples1 = dist1.sample(torch.Size([n_samples//2]))
samples = torch.vstack((samples0, samples1))
mean = torch.mean(samples, dim=0)
std = torch.std(samples, dim=0)
normalized_samples = (samples - mean[None, :])/std[None, :]使用する\(\boldsymbol{x}\)を2Dのヒストグラムで可視化すると以下のようになります。
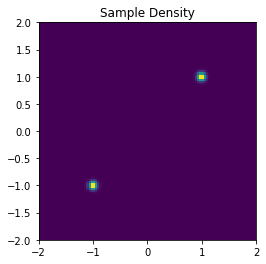
次にスコア関数のモデルと学習コードです。基本的には先ほど紹介したロス関数を使ってモデルを学習形になります。
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
class ScoreModel(nn.Module):
def __init__(self, sigma_min, sigma_max, n_channels=2):
super(ScoreModel, self).__init__()
self.sigma_min = sigma_min
self.sigma_max = sigma_max
self.model = nn.Sequential(
nn.Linear(n_channels, 2*n_channels),
nn.ELU(),
nn.Linear(2*n_channels, 16*n_channels),
nn.ELU(),
nn.Linear(16*n_channels, 2*n_channels),
nn.ELU(),
nn.Linear(2*n_channels, n_channels),
)
def forward(self, x, t):
y = self.model(x)
sigma_t = sigma(t=t, sigma_min=self.sigma_min, sigma_max=self.sigma_max)
return y/sigma_t
batch_size = 512
n_steps = 100000
dataloader = torch.utils.data.DataLoader(dataset, batch_size=512, shuffle=True, num_workers=0)
dataloader_iter = iter(dataloader)
score_model = ScoreModel(sigma_min=sigma_min, sigma_max=sigma_max).to(device)
optimizer = torch.optim.Adam(score_model.parameters())
lr_scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=0.001, total_steps=n_steps)
for i in range(n_steps):
try:
x = next(dataloader_iter)[0]
except StopIteration:
dataloader_iter = iter(dataloader)
x = next(dataloader_iter)[0]
x = x.to(device)
optimizer.zero_grad()
loss = dsm_loss(score_model, x, sigma_min=sigma_min, sigma_max=sigma_max)
loss.backward()
optimizer.step()
lr_scheduler.step()
if (i % 1000) == 0:
print(f"{i} steps loss:{loss}")学習が終わったら最後に以下のようにサンプリングする関数を呼び出してサンプリングします。
samples_pred = euler_maruyama_sample(n_samples=100000, score_model=score_model)サンプリングされたデータの2Dのヒストグラムは以下の通りです。
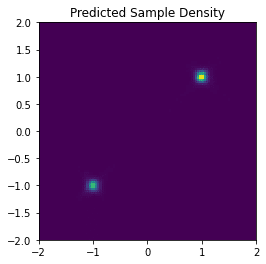
ほぼ元の分布と同じサンプリングが得られることが確認できました。
終わりに
今回は「拡散モデル データ生成技術の数理」の中で紹介されている分散発散型確率微分方程式 (VE-SDE)の部分を紹介しました。コードは先月の中旬にはできていたのですが、今回紹介する部分の式変形でぱっと見てわからないところがいくつかあり、それを調べていたらだいぶ時間がかかりました。また、説明のために必要な式の打ち込みにもかなり時間がかかってしまいました。
ただ、頑張ったおかげでかなりVE-SDEの部分の理解が進んだので記事にまとめてよかったです。
今後に関してはVP-SDEに関してもやろうと思っていますが、先に最近流行りのChatGPT, LLM, LangChainあたりに関していろいろ調べてみようと思うのでそちらの記事をいくつか書いてからになると思います。
この記事が他の方の役に少しでもなれば幸いです。
参考文献
- 確率微分方程式 入門から応用まで
- Särkkä, S., & Solin, A. (2019). Applied Stochastic Differential Equations (Institute of Mathematical Statistics Textbooks). Cambridge: Cambridge University Press. doi:10.1017/9781108186735
- Song, Y., Sohl-Dickstein, J.N., Kingma, D.P., Kumar, A., Ermon, S., & Poole, B. (2020). Score-Based Generative Modeling through Stochastic Differential Equations. ArXiv, abs/2011.13456.

