[勉強ノート] 「拡散モデル データ生成技術の数理」 2.2 スコアベースモデル
先日紹介した「拡散モデル データ生成技術の数理」をちゃんと理解するために数式を改めて追ったり、説明されているアルゴリズムを実装したりしています。
その第2弾として「2.2 スコアベースモデル」で説明されているスコアベースモデルの学習とそれを使ったサンプリングについてPython(深層学習部分はPytorch)でコードを書いて試したのでそのまとめになります。
また、この本を買うか迷っている方は私が読んだ感想をこちらの記事に書いてますので参考にしてみてください。
また、この記事で紹介したコードは以下にあげてありますので、コード全体を確認したい方はこちらをご覧ください。
スコアベースモデルとは
1章で紹介されているデノイジングスコアマッチングは以下の2つの問題点があると本では紹介されています。
- デノイジングスコアマッチングで推定されたスコア関数はデータ分布の密度が小さい領域で不正確
- データ分布が多峰性を持つ場合、あるモード(確率が大きい領域)から他のモードに移る際、確率が小さい領域を通過するために非常に多くのステップを必要とする
これらの問題を解決するためにスコアベースモデル(SBM)[1, 2] では複数の異なる強度のノイズによって攪乱した攪乱後分布を用意して、それらの攪乱後分布上のスコアを求めるようにしています。
スコアベースモデルの学習
スコア関数 \(s_{\theta}(\boldsymbol{x}, \sigma_t)\) を学習する際は以下のロス関数を使います。
$$ \begin{align*}
L_{\text{SBM}}(\theta) := \sum_{t=1}^T w_t E_{p_{\sigma_t}}(\tilde{\boldsymbol{x}}) \left\{ \left\| \nabla_{\tilde{\boldsymbol{x}}} \log p_{\sigma_t}(\tilde{\boldsymbol{x}}) – s_{\theta}(\tilde{\boldsymbol{x}}, \sigma_t) \right\|^2 \right\} \tag{2.2.1}
\end{align*} $$
ここで\(\sigma_t \) はノイズの強さを表す変数で\( \sigma_{min} = \sigma_1 < \sigma_2 <… < \sigma_T = \sigma_{max}\)の合計\(T\)個をスコアベースモデルでは利用します。そして、\(p_{\sigma_t}(\tilde{\boldsymbol{x}}) \) \(x\)は\(x\)の分布\(p(x)\)を\(\sigma_t\)の強さで攪乱したあとの分布を表しています。
この式(2.2.1)を本の1.5.5の「デノイジングスコアマッチング」で説明されている通り、デノイジングスコアマッチングを使って式を書き換えると以下のようになります。
$$ \begin{align*}
L_{\text{DSM-SBM}}(\theta) := \sum_{t=1}^T w_t E_{\boldsymbol{x} \sim p_{data}(\boldsymbol{x}),\tilde{\boldsymbol{x}} \sim \mathcal{N}(\boldsymbol{x}, \sigma_t^2\boldsymbol{I})} \left\{ \left\| \frac{\boldsymbol{x} – \tilde{\boldsymbol{x}}}{\sigma_t^2} – s_{\theta}(\tilde{\boldsymbol{x}}, \sigma_t) \right\|^2 \right\} \tag{2.2.2}
\end{align*} $$
詳細は本にわかりやすくかいてあるので本を参照してください。
ここで本の式(1.9)のデノイジングスコアマッチングの式において最初に\(1/2\)があるのに式(2.2.2)ではそれが省略されています。これに関して本にはちゃんと書いてない気がしますが、おそらくこれは\(w_t\)の中に\(1/2\)が含まれているから、もしくは\(1/2\)は定数であり、最適化の際にパラメータが移動する方向は\(1/2\)のありなしで変わらないということで省略しているのではないかと思っています。
ここから2章にはちゃんと書いてないですが、Pythonで実装するためにさらに式変形していきます。\(\tilde{\boldsymbol{x}} \sim \mathcal{N}(\boldsymbol{x}, \sigma_t^2\boldsymbol{I})\)なので、\(\tilde{\boldsymbol{x}}\)を\(\epsilon \sim \mathcal{N}(0, \sigma_t^2 \boldsymbol{I})\)を使って表すと以下のようになります。
$$ \begin{align*}
\tilde{\boldsymbol{x}} = \boldsymbol{x} + \epsilon \tag{2.2.3}
\end{align*} $$
この式(2.2.3)を使って式(2.2.2)を式変形すると以下の通りです。
$$ \begin{align*}
L_{\text{DSM-SBM}}(\theta) :=& \sum_{t=1}^T w_t E_{\boldsymbol{x} \sim p_{data}(\boldsymbol{x}),\tilde{\boldsymbol{x}} \sim \mathcal{N}(\boldsymbol{x}, \sigma_t^2\boldsymbol{I})} \left\{ \left\| \frac{\boldsymbol{x} – \tilde{\boldsymbol{x}}}{\sigma_t^2} – s_{\theta}(\tilde{\boldsymbol{x}}, \sigma_t) \right\|^2 \right\} \\
=& \sum_{t=1}^T w_t E_{\boldsymbol{x} \sim p_{data}(\boldsymbol{x}),\epsilon \sim \mathcal{N}(\boldsymbol{x}, \sigma_t \boldsymbol{I})} \left\{ \left\| \frac{-\epsilon}{\sigma_t^2} – s_{\theta}(\tilde{\boldsymbol{x}}, \sigma_t) \right\|^2 \right\} \tag{2.2.4}
\end{align*} $$
この式を見たときに\(t=1\)から\(t=T\)までの和をとっている部分、\(T\)のサイズによっては計算量がすごいことにならないか?ということを思いました。このため、何か実装するときに工夫があるのかも?ということで[2]著者実装である[3]を見にいきました。すると2023/03/03時点では\(t=1\)から\(t=T\)ランダムに\(t\)を選び、その平均をとるということをしていました。
Pythonのコードのほうが分かりやすいと思うので、以下にPythonのコードも示しておきます。
def dsm_loss(score_model, samples, sigmas):
t = torch.randint(0, len(sigmas), (samples.shape[0],), device=sigmas.device)
used_sigmas = sigmas[t].view(samples.shape[0], *([1] * len(samples.shape[1:])))
noise = torch.randn_like(samples) * used_sigmas
perturbed_samples = samples + noise
target = - 1 / (used_sigmas ** 2) * noise
scores = score_model(perturbed_samples, used_sigmas)
target = target.view(target.shape[0], -1)
scores = scores.view(scores.shape[0], -1)
w = used_sigmas.squeeze(-1) ** 2
loss = ((scores - target) ** 2).sum(dim=-1) * w
return loss.mean()ここでscore_modelがスコア関数 \(s_{\theta}(\boldsymbol{x}, \sigma_t )\) 、samplesが\(\boldsymbol{x}\)、sigmasが\(\{\sigma_1,…,\sigma_T\}\)の配列となっています。また、\(w_t\)は本にならって\(w_t=\sigma_t^2\)を使っています。
この関数では最初にランダムに\(t\)を選び、それに従ってノイズを生成し、\(\tilde{\boldsymbol{x}}\)を作ります。その後、スコア関数のscore_modelを使ってスコアを計算し、式(2.2.4)を使ってロス関数を計算します。
このロス関数を使ってスコア関数のパラメータを学習していきます。
ここで1つ、スコア関数のモデルに関して注意点があります。スコア関数は\(s_{\theta}(\boldsymbol{x}, \sigma_t) \)は\(\boldsymbol{x}\)だけでなく\(\sigma_t\)も引数にとります。このため、モデルの中でどうにかして\(\sigma_t \)と\(\boldsymbol{x}\)の入力を組み合わせる必要があります。これに関して今回のコードでは[3]の実装にならって、以下のようにして\(\boldsymbol{x}\)だけを入力として受け取るスコア関数\(s_{\theta}^{\prime}(\boldsymbol{x})\)の出力を\(\sigma_t\)で割るという形にしています。
$$ \begin{align*}
s_{\theta}(\boldsymbol{x}, \sigma_t) = s_{\theta}^{\prime}(\boldsymbol{x}) / \sigma_t \tag{2.2.5}
\end{align*} $$
また、後ほど示しますが、今回は2つのガウス分布の混合分布を入力とします。この分布はシンプルな分布なため、今回は簡単なMLPをスコア関数のモデル使用します。コードとては以下のようになります。
import numpy as np
import torch
import torch.nn as nn
import torch.nn.functional as F
class ScoreModel(nn.Module):
def __init__(self, n_channels=2):
super(ScoreModel, self).__init__()
self.model = nn.Sequential(
nn.Linear(n_channels, 2*n_channels),
nn.ELU(),
nn.Linear(2*n_channels, 16*n_channels),
nn.ELU(),
nn.Linear(16*n_channels, 2*n_channels),
nn.ELU(),
nn.Linear(2*n_channels, n_channels),
)
def forward(self, x, sigma):
y = self.model(x)
return y/sigmaスコアベースモデルを使ったサンプリング
ここから学習済みのスコア関数\(s_{\theta}(\boldsymbol{x}, \sigma_t) \)を使ったサンプリングについて説明していきます。
スコアベースモデルを使ったサンプリング1章で紹介されたランジュバン・モンテカルロ法をベースにしています。ランジュバン・モンテカルロ法の部分についてはこちらに解説しています。
詳細は上の記事にかいてありますが、ランジュバン・モンテカルロ法は最初、ランダムに\(\boldsymbol{x}_0\)を生成後、以下のランジュバン・モンテカルロ法の更新則を\(K\)回繰り返すことで\(p(\boldsymbol{x})\)からサンプリングしたようなデータを作ります。
$$ \begin{align*}
\boldsymbol{x}_k := \boldsymbol{x}_{k-1} + \alpha \nabla_\boldsymbol{x} \log p(\boldsymbol{x}_{k-1}) + \sqrt{2\alpha}\boldsymbol{u}_k \tag{2.2.6}
\end{align*} $$
スコアベースモデルのサンプリングでは更新則のスコア(\(\nabla_\boldsymbol{x} \log p(\boldsymbol{x}_{k-1})\))を学習したスコア関数に置き換えた以下の更新則を利用します。
$$ \begin{align*}
\boldsymbol{x}_{t, k} := \boldsymbol{x}_{t, k-1} + \alpha_t s_{\theta}(\boldsymbol{x}_{t, k-1}, \sigma_t)+ \sqrt{2\alpha_t}\boldsymbol{u}_k \tag{2.2.7}
\end{align*} $$
この更新則を用いたスコアベースモデルのサンプリングの疑似コードは以下の通りです。(「拡散モデル データ生成技術の数理」Algorithm 2.1の引用)
- \(\boldsymbol{x}_0\)を初期化(\(\boldsymbol{x}_0 \sim \mathcal{N}(0, \sigma_T^2 \boldsymbol{I})\))
- for \(t=1,…,T\) do
- \(\quad \alpha_t := \alpha \sigma_t^2\/\sigma_T^2)\
- \(\quad\) for \(k=1,…,K\) do
- \(\qquad \boldsymbol{u}_k \sim \mathcal{N}(0, \boldsymbol{I})\)
- \(\qquad\) if \(t=1\) and \(k=K\) then \(\boldsymbol{u}_k := 0\)
- \(\qquad \boldsymbol{x}_{t, k} := \boldsymbol{x}_{t, k-1} + \alpha_t s_{\theta}(\boldsymbol{x}_{t, k-1}, \sigma_t)+ \sqrt{2\alpha_t}\boldsymbol{u}_k \)
- \(\quad\) end for
- \(\quad \boldsymbol{x}_{t-1, 0} := \boldsymbol{x}_{t, K}\)
- end for
- return \(\boldsymbol{x}_{0, 0}\)
ここで\(\alpha\)はステップ幅のスケール、\(K\)はステップ回数です。アルゴリズムを見て分かる通り、ノイズの強度を変えながらランジュバン・モンテカルロ法を使って少しずつ\(\boldsymbol{x}_{t, k}\)を変化させています。また、7行目にある通り、各ノイズの強度の最後のステップではデノイジングのみを行うことでサンプリングの品質を向上させています。
この疑似コードをPythonのコードにするとこのようになります。
def sbm_sample(n_samples, score_model, sigmas, alpha=0.1):
sigma_T = sigmas[-1]
x_0 = torch.randn(n_samples, 2)*sigma_T
x_tk = x_0
K = 200
for t in range(len(sigmas) -1, -1, -1):
sigma_t = sigmas[t]
alpha_t = alpha*(sigma_t**2)/(sigma_T**2)
print(f"t:{t}, sigma_t:{sigma_t}, alpha_t:{alpha_t}")
for k in range(K+1):
u_k = torch.randn(n_samples, 2)
if (k == K) and t == 0:
u_k[:, :] = 0.0
with torch.no_grad():
score = score_model(x_tk, sigma_t)
x_tk = x_tk + alpha_t * score + np.sqrt(2 * alpha_t) * u_k
return x_tkn_samplesが生成するサンプル数、score_modelがスコア関数、sigmasがノイズ強度の配列、alphaがステップ幅のスケールになっています。
実行例
先ほど紹介したPythonコードを実際に動かした例も示しておきます。参考例として入力となる\(\boldsymbol{x}\)のサンプリングする分布の確率密度関数は以下のように平均が違うガウス分布二つの混合分布とし、サンプリングしたデータを正規化して使用します。
n_samples = int(1e6)
sigma = 0.01
dist0 = torch.distributions.MultivariateNormal(torch.tensor([-2, -2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples0 = dist0.sample(torch.Size([n_samples//2]))
dist1 = torch.distributions.MultivariateNormal(torch.tensor([2, 2], dtype=torch.float).to(device), sigma*torch.eye(2, dtype=torch.float).to(device))
samples1 = dist1.sample(torch.Size([n_samples//2]))
samples = torch.vstack((samples0, samples1))
mean = torch.mean(samples, dim=0)
std = torch.std(samples, dim=0)
normalized_samples = (samples - mean[None, :])/std[None, :]使用する\(\boldsymbol{x}\)を2Dのヒストグラムで可視化すると以下のようになります。
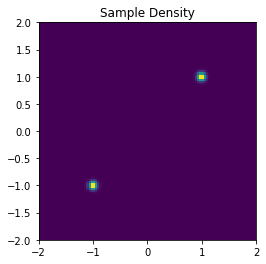
このデータを再現できるようにスコア関数を学習します。学習コードは以下の通りです。
import torch
batch_size = 512
n_steps = 100000
dataset = torch.utils.data.TensorDataset((normalized_samples))
dataloader = torch.utils.data.DataLoader(dataset, batch_size=512, shuffle=True, num_workers=0)
dataloader_iter = iter(dataloader)
score_model = ScoreModel().to(device)
optimizer = torch.optim.Adam(score_model.parameters())
lr_scheduler = torch.optim.lr_scheduler.OneCycleLR(optimizer, max_lr=0.001, total_steps=n_steps)
for i in range(n_steps):
try:
x = next(dataloader_iter)[0]
except StopIteration:
dataloader_iter = iter(dataloader)
x = next(dataloader_iter)[0]
x = x.to(device)
optimizer.zero_grad()
loss = dsm_loss(score_model, x, sigmas)
loss.backward()
optimizer.step()
lr_scheduler.step()
if (i % 1000) == 0:
print(f"{i} steps loss:{loss}")学習が終わったら、以下のようにして学習したモデルを利用してサンプリングします。
samples_pred = sbm_sample(n_samples=100000, score_model=score_model, sigmas=sigmas)サンプリングされたデータの2Dのヒストグラムは以下の通りです。
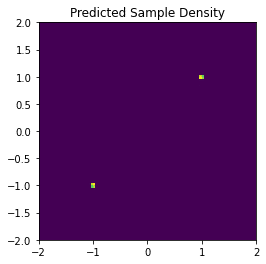
可視化結果をみると元の分布の平均の近くにデータが集中しているので、うまくいっていると考えられます。
ただ、やってみるとわかるのですがちゃんとした結果を得るために人手で決めないといけないハイパーパラメータの選択が難しい印象です。この結果もかなり試行錯誤してなんとかこの結果を作ることができたというイメージです。
終わりに
今回は「拡散モデル データ生成技術の数理」の2.2のスコアベースモデルの説明の部分のコードを書いたのでそのまとめの記事になります。最初、MNISTのデータでやろうとして、MNISTのデータを学習できるコードを説明するのは結構大変、ということでシンプルな混合ガウス分布にしました。ただ、それでも結構な分量になった印象です。ちなみに次のDDPMも紹介用のコードはできているので、近日中に記事を書いて公開しようと思います。
この記事が少しでもみなさんの理解の助けになれば幸いです。
参考文献
- Song, Y., & Ermon, S. (2019). Generative Modeling by Estimating Gradients of the Data Distribution. ArXiv, abs/1907.05600.
- Song, Y., & Ermon, S. (2020). Improved Techniques for Training Score-Based Generative Models. ArXiv, abs/2006.09011.
- https://github.com/ermongroup/ncsnv2

