JAXによる微分可能Smith Watermanアルゴリズムのパフォーマンス測定
最近微分可能な Smith Waterman アルゴリズムというものとJAXのコードが公開されました。今回はこれらを参考に、JAXの勉強がてら何パターンかSmith Watermanアルゴリズムを実装して測定してみたので、その結果のまとめの紹介となります。
論文は以下のものです。
[1] Petti, S., Bhattacharya, N., Rao, R., Dauparas, J., Thomas, N., Zhou, J., … Ovchinnikov, S. (2021). End-to-end learning of multiple sequence alignments with differentiable Smith-Waterman. BioRxiv, 2021.10.23.465204. https://doi.org/10.1101/2021.10.23.465204
また、著者の実装はこちらに公開されています。
https://github.com/spetti/SMURF
今回は主に私がJAXの勉強をしたかったということもあり、いくつか実装を作ってパフォーマンスを測定して、「JAXって速いの?」という疑問にある程度答えられればと思い、記事を書いています。今回の実装はすべてこちらにありますので参考にしてみてください。
https://github.com/shu65/blog-jax-notebook/blob/main/JAX_Smooth_Smith_Waterman.ipynb
また、計算時間測定はすべてGoogle Cloab上のCPUで行っています。
目次
論文概要
この論文では教師なし学習によるコンタクト予測において、前処理で使われるSmith Watermanアルゴリズムを微分可能なものに置き換えて、Smith Watermanアルゴリズムの中で使われるパラメータ(置換スコア)も含めて学習する手法 SMURFを提案した論文です。論文自体にはコンタクト予測の精度なども書かれていますが、微分可能なSmith Watermanの紹介をメインにしたいため、今回は割愛します。
微分可能な Smith Waterman アルゴリズム「Smooth Smith Waterman」とは?
Smith Watermanアルゴリズムを微分可能にするためには、微分可能ではない関数を微分可能なものに置き換えて、近似することで実現します。まずは大本のSmith Watermanアルゴリズムの説明をしたあと、微分可能なものに変更する方法を紹介していきます。
Smith Watermanアルゴリズムとは
Smith Watermanアルゴリズム は2つのDNAやタンパク質の配列の類似度、特にローカルアライメントのスコアと呼ばれる類似度を計算するアルゴリズムです。ローカルアラインメントとは2配列間の類似度の高い部分的な文字列を発見するときに使われます。これは以下のように行列の要素を計算する動的計画法 (Dynamic Programming, DP) により計算します。
$$ H_{i0} = H_{0j} = 0 \\ H_{ij} = \max\begin{cases} H_{i-1,j-1} + s(a_i,b_j), \\ H_{i-k,j} + g, \\ H_{i,j-l} +g, \\
0 \\
\end{cases} $$
\( s(a_i,b_j) \) は 配列Aのi番目の文字と配列Bのj番目の文字の置換スコアと呼ばれるもので、同じ文字、もしくは類似度の高い文字のペアはプラス、類似度の低い文字のペアはマイナスにするのが一般的です。また、 \( g \) はギャップペナルティと呼ばれるもので、1文字飛ばしのペナルティを表します。
Smith Watermanアルゴリズムを微分可能にする
先ほど説明したとおり、Smith Watermanアルゴリズムではmax関数があります。この部分が微分可能ではないため、SmithWatermanアルゴリズムは微分可能ではありません。このため、このmax関数を微分可能な何等かの関数で置き換える必要があります。この論文ではmax関数を「logsumexp」で置き換えることで微分可能にします。
logsumexpはmax関数を滑らかに近似するための関数として使われる関数で、微分可能な関数です。このためmax関数を logsumexp に置き換えればSmith Watermanアルゴリズムの計算全体が微分可能になります。論文中ではこの微分可能なSmtth Watermanアルゴリズムを「Smooth Smith Waterman」と呼んでいます。
なぜlogsumexpがmax関数の近似になるかを詳しく知りたい方は、こちらのブログ記事がわかりやすかったのでお勧めです。
numpyによるシンプルな Smooth Smith Waterman
後ほどJAXの実装を示しますが、高速化したあとのJAXのコードは初見では分かりづらいため、先にシンプルなnumpyの実装を示します。この実装は著者の実装にあわせつつ、numpyとのパフォーマンス実装をするために以下のようにしています。
- 配列Aと配列Bの全文字ペアの置換スコアの行列
score_matrix(置換スコアの行列のサイズは|A|×|B|)と2つの配列の長さlengths、その他のパラメータを入力とする - この記事では勾配を計算できないnumpyとの比較のために、著者実装では
score_matrixの勾配を返すのに対して、今回の記事では2配列の最大スコアを返す。
Smith Watermanアルゴリズムをご存じの方は戸惑うかもしれませんが、Smooth Smith Watermanアルゴリズムではscore_matrixの勾配を出力として返す関数になっています。このため、あらかじめ配列Aと配列Bの全文字ペアの置換スコアの行列を用意して入力にします。
このため、配列Aと配列Bは入力に出てきませんし、PAMやBLOSUMなどの置換スコアもでてきません。
このSmooth Smith Watermanアルゴリズムをシンプルにnumpyで実装すると以下の通りになります。
def sw_np(NINF=-1e30):
def _logsumexp(y, axis):
y = np.maximum(y,NINF)
return y.max(axis) + np.log(np.sum(np.exp(y - y.max(axis, keepdims=True)), axis=axis))
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _sw(score_matrix, lengths, gap=0, temp=1.0):
real_a, real_b = lengths
hij = np.full((real_a + 1, real_b + 1), fill_value=NINF, dtype=np.float32)
for i in range(real_a):
for j in range(real_b):
s = score_matrix[i, j]
m = hij[i, j] + s
g0 = hij[i + 1, j] + gap
g1 = hij[i, j + 1] + gap
h = np.stack([m, g0, g1, s], -1)
hij[i + 1, j + 1] = _soft_maximum(h, temp=temp, axis=-1)
hij = hij[1:, 1:]
score = _soft_maximum(hij, temp=temp)
return score
return _swこちらの実装で通常のSmith Watermanアルゴリズムと違う点は以下の2点です
- DPの行列の要素更新のところでmax関数をlogsumexpで実装した
_soft_maximum()という関数に置き換えている。 - DPの行列の各要素を入れるところで最大値を取るところで0以下にならないようにmax関数の入力の一つとして0を入れるところを、置換スコア(
s)を入れている。
1が微分可能とするための改良した箇所です。一方、2に関しては私が読み飛ばしてしまった可能性がありますが、特に論文中に説明が見当たらなかった変更点です。なんとなくSmooth Smith Watermanアルゴリズムを使って深層学習のモデル更新をするときにうまく勾配が置換スコアに流れるようにするためでは?と思っているのですが、未確認な状態です。何かご存じの方がいれば教えていただければと思っています。
この実装を実行したときの計算時間を%timeで測定すると以下の通りです。
CPU times: user 735 ms, sys: 4 ms, total: 739 ms Wall time: 743 ms
JAXを使ったSmooth Smith アルゴリズム
ここからnumpyの部分をJAXに置き換えてSmooth Smith Watermanアルゴリズムを実装し、徐々に改良していくという順番で説明していきます。まずはJAXをご存じない方のためにJAXを簡単に説明します。
JAXってなに?
JAXはPythonやnumpyの関数を微分可能なものにし、XLAというコンパイラを使ってGPUやTPUで実行で実行できるようにしたライブラリです。
JAXでは勾配が計算できることと、jitをはじめとした様々な高速化する仕組みが用意されているため、最近論文で利用しているケースが増えてきた印象です。特に今回紹介した論文のような、従来では微分可能でなかった計算を微分可能なものに置き換え、深層学習のモデル学習の中で利用するという手法の実装にJAXが使われるのをよく目にします。今回紹介したものの他には BRAXがあります。
https://github.com/google/brax
単純なJAX実装
JAXはnumpyの関数と同じAPIの関数があるので、まずはそれをそのまま利用してみます。
def sw_v0(NINF=-1e30):
def _logsumexp(y, axis):
y = jnp.maximum(y,NINF)
return jax.nn.logsumexp(y, axis=axis)
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _sw(score_matrix, lengths, gap=0, temp=1.0):
real_a, real_b = lengths
hij = jnp.full((real_a + 1, real_b + 1), fill_value=NINF, dtype=jnp.float32)
for i in range(real_a):
for j in range(real_b):
s = score_matrix[i, j]
m = hij[i, j] + s
g0 = hij[i + 1, j] + gap
g1 = hij[i, j + 1] + gap
h = jnp.stack([m, g0, g1, s], -1)
hij = hij.at[i + 1, j + 1].set(_soft_maximum(h, -1))
hij = hij[1:, 1:]
score = _soft_maximum(hij)
return score
return _swこれも動くには動くのですが、あまりにも遅いため、まったく使い物になりません。このためJAXを使う際はもう少し真面目に高速に動くアルゴリズムで実装する必要があります。
Striped Smith-Watermanベースの実装
論文でも紹介されているStriped Smith-Watermanベースで実装してみます。 Smith-Waterman アルゴリズムをSIMDなどで並列化する方法として、依存関係のないDP行列の斜めのセルを同時に埋めていくという方法がしばしば取られます。詳しくはこちらをご覧ください。
Farrar, M. (2007). Striped Smith-Waterman speeds database searches six times over other SIMD implementations. Bioinformatics (Oxford, England), 23(2), 156–161. https://doi.org/10.1093/bioinformatics/btl582
これをJAXで実装するにあたり、著者はDP行列を回転させ、依存関係のない斜めに並んだセルを横1列に並べて計算するようにしています。
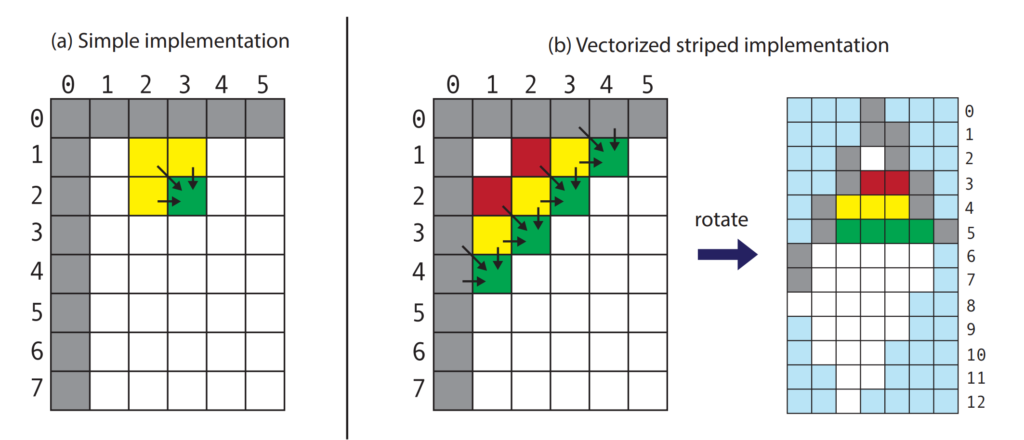
こうすることで内側のforループをJAXのベクトルの計算で実行できるようにしています。個人的にはここがこの論文の最大の貢献な気がしています。具体的にJAXで実装すると以下の通りです。
def sw_v1(unroll=2, NINF=-1e30):
def _rotate(score_matrix):
a,b = score_matrix.shape
n,m = (a+b-1),(a+b)//2
ar,br = jnp.arange(a)[::-1,None], jnp.arange(b)[None,:]
i,j = (br-ar)+(a-1),(ar+br)//2
rotated_score_matrix = jnp.full([n,m],NINF).at[i,j].set(score_matrix)
reverse_idx = (i, j)
return rotated_score_matrix, reverse_idx
def _rotate_in_reverse(rotated_dp_matrix, reverse_idx):
return rotated_dp_matrix[reverse_idx]
def _logsumexp(y, axis):
y = jnp.maximum(y,NINF)
return jax.nn.logsumexp(y, axis=axis)
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _step(prev, gap_cell_condition, rotated_score_matrix, gap, temp):
h2,h1 = prev # previous two rows of scoring (hij) mtx
h1_T = jax.lax.cond(
gap_cell_condition,
lambda x: jnp.pad(x[:-1], [1,0], constant_values=(NINF,NINF)),
lambda x: jnp.pad(x[1:], [0,1], constant_values=(NINF,NINF)),
h1,
)
a = h2 + rotated_score_matrix
g0 = h1 + gap
g1 = h1_T + gap
s = rotated_score_matrix
h0 = jnp.stack([a, g0, g1, s], -1)
h0 = _soft_maximum(h0, temp, -1)
return (h1,h0), h0
def _sw(score_matrix, lengths, gap=0, temp=1.0):
rotated_score_matrix, reverse_idx = _rotate(score_matrix)
a,b = score_matrix.shape
n,m = rotated_score_matrix.shape
gap_cell_condition = (jnp.arange(n)+a%2)%2
prev = (jnp.full(m, NINF), jnp.full(m, NINF))
rotated_hij = []
for i in range(n):
prev, h = _step(prev, gap_cell_condition[i], rotated_score_matrix[i], gap, temp)
rotated_hij.append(h)
rotated_hij = jnp.stack(rotated_hij)
hij = _rotate_in_reverse(rotated_hij, reverse_idx)
score = _soft_maximum(hij, temp=temp)
return score
return _swこの実装では置換行列score_matrixを回転させて、DP行列のセルを埋めていき、そのあとDP行列元の方向に戻すということをしています。
回転させたときの注意点として、DP行列の列番号が偶数か奇数かでギャップペナルティのスコアを加算するセルの相対座標が変わります。このため、jax.lax.cond()を利用して使うセルを分岐しています。
この実装をそのまま実行したときとjitを利用したときの計算時間は以下の通りです。
jax default first call CPU times: user 17.7 s, sys: 177 ms, total: 17.8 s Wall time: 17.8 s jax default second call CPU times: user 17.6 s, sys: 153 ms, total: 17.7 s Wall time: 17.7 s jax jit first call CPU times: user 2min 20s, sys: 715 ms, total: 2min 21s Wall time: 2min 20s jax jit second call CPU times: user 1.98 ms, sys: 0 ns, total: 1.98 ms Wall time: 1.81 ms
jitなしでそのまま実行するのはnumpyよりもかなり遅い印象です。またjitを使う場合も最初の呼び出しはコンパイルが走ることもあり、jitなしに比べるとさらに遅くなっています。さすがに1回目とはいえ、ここまで時間がかかると使いづらいと思われます。このため、まだ工夫する必要があります。
外側のforループをjax.lax.scan()に置き換える
1つ前の実装で遅い原因がどこか?というとforループです。これを速くする方法としてJAXのforループと類似する処理を実行するための関数を利用します。今回はforループ部分を jax.lax.scan() に置き換えます。
実装は以下の通りです。
def sw_v2(unroll=2, NINF=-1e30):
def _rotate(score_matrix):
a,b = score_matrix.shape
n,m = (a+b-1),(a+b)//2
ar,br = jnp.arange(a)[::-1,None], jnp.arange(b)[None,:]
i,j = (br-ar)+(a-1),(ar+br)//2
rotated_score_matrix = jnp.full([n,m],NINF).at[i,j].set(score_matrix)
reverse_idx = (i, j)
return rotated_score_matrix, reverse_idx
def _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp):
def scan_f(prev, scan_xs):
h2, h1 = prev
h1_T = jax.lax.cond(
scan_xs["gap_cell_condition"],
lambda x: jnp.pad(x[:-1], [1,0], constant_values=(NINF,NINF)),
lambda x: jnp.pad(x[1:], [0,1], constant_values=(NINF,NINF)),
h1,
)
a = h2 + scan_xs["rotated_score_matrix"]
g0 = h1 + gap
g1 = h1_T + gap
s = scan_xs["rotated_score_matrix"]
h0 = jnp.stack([a, g0, g1, s], -1)
h0 = _soft_maximum(h0, temp, -1)
return (h1,h0), h0
a,b = score_matrix.shape
n,m = rotated_score_matrix.shape
scan_xs = {
"rotated_score_matrix": rotated_score_matrix,
"gap_cell_condition": (jnp.arange(n)+a%2)%2
}
scan_init = (jnp.full(m, NINF), jnp.full(m, NINF))
return scan_f, scan_xs, scan_init
def _rotate_in_reverse(rotated_dp_matrix, reverse_idx):
return rotated_dp_matrix[reverse_idx]
def _logsumexp(y, axis):
y = jnp.maximum(y,NINF)
return jax.nn.logsumexp(y, axis=axis)
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _sw(score_matrix, lengths, gap=0, temp=1.0):
rotated_score_matrix, reverse_idx = _rotate(score_matrix)
scan_f, scan_xs, scan_init = _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp)
rotated_hij = jax.lax.scan(scan_f, scan_init, scan_xs, unroll=unroll)[-1]
hij = _rotate_in_reverse(rotated_hij, reverse_idx)
score = _soft_maximum(hij, temp, axis=None)
return score
return _swこの実装でforループがなくなりました。実行した結果は以下の通りです。
jax default first call CPU times: user 739 ms, sys: 18 ms, total: 757 ms Wall time: 758 ms jax default second call CPU times: user 666 ms, sys: 1.98 ms, total: 668 ms Wall time: 671 ms jax jit first call CPU times: user 1 s, sys: 5.01 ms, total: 1.01 s Wall time: 1.01 s jax jit second call CPU times: user 339 µs, sys: 989 µs, total: 1.33 ms Wall time: 1.14 ms
先ほどに比べるとjitなしでも速くなりましたが、jitありの1回目の実行もかなり速くなった印象です。これなら十分使えるのではないか?と思っています。
jax.lax.condの置き換え
著者の実装では jax.lax.cond()を使わずに加算と乗算だけで実装されています。試しに同様の実装にしたバージョンも示します。具体的な実装は以下の通りです。
def sw_v3(unroll=2, NINF=-1e30):
def _rotate(score_matrix):
a,b = score_matrix.shape
n,m = (a+b-1),(a+b)//2
ar,br = jnp.arange(a)[::-1,None], jnp.arange(b)[None,:]
i,j = (br-ar)+(a-1),(ar+br)//2
rotated_score_matrix = jnp.full([n,m],NINF).at[i,j].set(score_matrix)
reverse_idx = (i, j)
return rotated_score_matrix, reverse_idx
def _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp):
def scan_f(prev, scan_xs):
h2, h1 = prev
h1_T = _get_prev_gap_cell_score(
scan_xs["gap_cell_condition"],
jnp.pad(h1[:-1], [1,0], constant_values=(NINF,NINF)),
jnp.pad(h1[1:], [0,1], constant_values=(NINF,NINF)),
)
a = h2 + scan_xs["rotated_score_matrix"]
g0 = h1 + gap
g1 = h1_T + gap
s = scan_xs["rotated_score_matrix"]
h0 = jnp.stack([a, g0, g1, s], -1)
h0 = _soft_maximum(h0, temp, -1)
return (h1,h0), h0
a,b = score_matrix.shape
n,m = rotated_score_matrix.shape
scan_xs = {
"rotated_score_matrix": rotated_score_matrix,
"gap_cell_condition": (jnp.arange(n)+a%2)%2
}
scan_init = (jnp.full(m, NINF), jnp.full(m, NINF))
return scan_f, scan_xs, scan_init
def _rotate_in_reverse(rotated_dp_matrix, reverse_idx):
return rotated_dp_matrix[reverse_idx]
def _logsumexp(y, axis):
y = jnp.maximum(y,NINF)
return jax.nn.logsumexp(y, axis=axis)
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _get_prev_gap_cell_score(cond, true, false):
return cond*true + (1-cond)*false
def _sw(score_matrix, lengths, gap=0, temp=1.0):
rotated_score_matrix, reverse_idx = _rotate(score_matrix)
scan_f, scan_xs, scan_init = _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp)
rotated_hij = jax.lax.scan(scan_f, scan_init, scan_xs, unroll=unroll)[-1]
hij = _rotate_in_reverse(rotated_hij, reverse_idx)
score = _soft_maximum(hij, temp, axis=None)
return score
return _swこの時のパフォーマンスは以下の通りです。
jax defaujax default first call CPU times: user 599 ms, sys: 1.99 ms, total: 601 ms Wall time: 608 ms jax default second call CPU times: user 599 ms, sys: 3.02 ms, total: 602 ms Wall time: 607 ms jax jit first call CPU times: user 940 ms, sys: 2.01 ms, total: 942 ms Wall time: 947 ms jax jit second call CPU times: user 4.9 ms, sys: 0 ns, total: 4.9 ms Wall time: 3.41 ms
jitなしの時は速くなっている印象ですが、jitありのときは少し遅くなっています。ただ、何度か実行してみると逆転することもあるようなので、誤差の範囲かもしれません。また、JAX特有のパフォーマンス測定のお作法をし忘れている可能性もあります。もしご存じの方があればコメントいただければと思います。
Batch実行用の実装
著者のSmooth Smith Watermanは2つの配列のペアを1つだけ実行するのではなく、複数のペアをまとめて実行することを想定されて実装してあります。ここでも同様に複数のペアをまとめて計算するのもやってみようと思います。
簡単な実装
複数のペアをまとめて実装する際、ペア毎に配列の長さが違っても動作するようにします。このため、置換スコアのうち必要な部分だけmaskするようにします。
実装は以下の通りです。
def sw_v4(unroll=2, NINF=-1e30):
def _make_mask(score_matrix, lengths):
a,b = score_matrix.shape
real_a, real_b = lengths
mask = (jnp.arange(a) < real_a)[:,None] * (jnp.arange(b) < real_b)[None,:]
return mask
def _rotate(score_matrix):
a,b = score_matrix.shape
n,m = (a+b-1),(a+b)//2
ar,br = jnp.arange(a)[::-1,None], jnp.arange(b)[None,:]
i,j = (br-ar)+(a-1),(ar+br)//2
rotated_score_matrix = jnp.full([n,m],NINF).at[i,j].set(score_matrix)
reverse_idx = (i, j)
return rotated_score_matrix, reverse_idx
def _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp):
def scan_f(prev, scan_xs):
h2, h1 = prev
h1_T = _get_prev_gap_cell_score(
scan_xs["gap_cell_condition"],
jnp.pad(h1[:-1], [1,0], constant_values=(NINF,NINF)),
jnp.pad(h1[1:], [0,1], constant_values=(NINF,NINF)),
)
a = h2 + scan_xs["rotated_score_matrix"]
g0 = h1 + gap
g1 = h1_T + gap
s = scan_xs["rotated_score_matrix"]
h0 = jnp.stack([a, g0, g1, s], -1)
h0 = _soft_maximum(h0, temp, -1)
return (h1,h0), h0
a,b = score_matrix.shape
n,m = rotated_score_matrix.shape
scan_xs = {
"rotated_score_matrix": rotated_score_matrix,
"gap_cell_condition": (jnp.arange(n)+a%2)%2
}
scan_init = (jnp.full(m, NINF), jnp.full(m, NINF))
return scan_f, scan_xs, scan_init
def _rotate_in_reverse(rotated_dp_matrix, reverse_idx):
return rotated_dp_matrix[reverse_idx]
def _logsumexp(y, axis):
y = jnp.maximum(y,NINF)
return jax.nn.logsumexp(y, axis=axis)
def _logsumexp_with_mask(y, axis, mask):
y = jnp.maximum(y,NINF)
return y.max(axis) + jnp.log(jnp.sum(mask * jnp.exp(y - y.max(axis, keepdims=True)), axis=axis))
def _soft_maximum(x, temp, axis=None):
return temp*_logsumexp(x/temp, axis)
def _soft_maximum_with_mask(x, temp, mask, axis=None):
return temp*_logsumexp_with_mask(x/temp, axis, mask)
def _get_prev_gap_cell_score(cond, true, false):
return cond*true + (1-cond)*false
def _sw(score_matrix, lengths, gap=0, temp=1.0):
mask = _make_mask(score_matrix, lengths)
masked_score_matrix = score_matrix + NINF * (1 - mask)
rotated_score_matrix, reverse_idx = _rotate(masked_score_matrix)
scan_f, scan_xs, scan_init = _prepare_scan_inputs(score_matrix, rotated_score_matrix, gap, temp)
rotated_hij = jax.lax.scan(scan_f, scan_init, scan_xs, unroll=unroll)[-1]
hij = _rotate_in_reverse(rotated_hij, reverse_idx)
score = _soft_maximum_with_mask(hij, temp, mask=mask, axis=None)
return score
return _swこの実装をペアの数分、forループで計算していくようにします。
def batch_sw_v0(NINF=-1e30):
def _batch_sw(batch_score_matrix, batch_lengths, gap=0, temp=1.0):
n_batches = batch_score_matrix.shape[0]
sw_func = jax.jit(sw_v4())
ret = [sw_func(batch_score_matrix[i], batch_lengths[i], gap, temp)
for i in range(n_batches)]
return jnp.array(ret)
return _batch_swこれを実行すると計算時間は以下の通りでした。
batch jax default first call CPU times: user 1.31 s, sys: 13 ms, total: 1.33 s Wall time: 1.32 s batch jax default second call CPU times: user 1.3 s, sys: 5.02 ms, total: 1.3 s Wall time: 1.3 s batch jax default first call CPU times: user 10min 43s, sys: 2.99 s, total: 10min 46s Wall time: 10min 45s batch jax default second call CPU times: user 279 ms, sys: 2 ms, total: 281 ms Wall time: 281 ms
forループでそのまま実装すると、jitありのときはやはり1度目の実行に非常に時間がかかるようです。このため、この部分を速くします。
forループをjax.vmap()で置き換える
ここではforループを jax.vmap() で置き換えます。
def batch_sw_v1(unroll=2, NINF=-1e30):
sw_func = sw_v4(unroll=unroll, NINF=NINF)
batch_sw_func = jax.vmap(sw_func, (0, 0, None, None))
return batch_sw_funcこの時の計算時間は以下の通りです。
batch jax default first call CPU times: user 1.04 s, sys: 11 ms, total: 1.05 s Wall time: 1.03 s batch jax default second call CPU times: user 1.04 s, sys: 7.97 ms, total: 1.04 s Wall time: 1.01 s batch jax default first call CPU times: user 1.51 s, sys: 10 ms, total: 1.52 s Wall time: 1.5 s batch jax default second call CPU times: user 120 ms, sys: 9 µs, total: 120 ms Wall time: 97 ms
先ほどと比べるとかなり高速化できました。ちなみにこれがほぼ著者の実装と同じものになります。
結果まとめ
ここまでの計算時間の結果をまとめると以下の通りです。
| jitなし1回目 | jitなし2回目 | jitあり1回目 | jitあり2回目 | |
| numpy | 739 ms | – | – | – |
| Striped Smith-Watermanベースの実装 | 17.8 s | 17.7 s | 2min 21s | 1.98 ms |
| 外側のforループをjax.lax.scan()に置き換える | 757 ms | 668 ms | 1.01 s | 1.33 ms |
| jax.lax.condの置き換え | 601 ms | 602 ms | 942 ms | 4.9 ms |
| jitなし1回目 | jitなし2回目 | jitあり1回目 | jitあり2回目 | |
| 簡単な実装 | 1.33 s | 1.3 s | 10min 46s | 281 ms |
| forループをjax.vmap()で置き換える | 1.05 s | 1.04 s | 1.52 s | 120 ms |
各実装を比較するとforループのありなしでかなり実行時間やコンパイル時間が変化していることがわかります。このためnumpyの実装をそのままJAXにすればそれだけで速くなることはまずなさそうです。また、何も考えずに実装してjitを使うと、コンパイル時間が長すぎて使い物にならないというケースが多そうな気がしています。このため、JAXを使いこなすにはどのような計算は遅いかを理解して使うことが重要そうな印象です。
おわりに
今回、初のJAX使用だったため、パフォーマンス測定や高速化にはもっとやり方があるかもしれないと思っています。もしお気づきの点がありましたら気兼ねなくコメントいただければと思っています。
次はできればJAXとPyTorchのjitとどちらが速いのか試せればと思っています。

