[勉強ノート] 入門 統計的因果推論 3章 介入効果　

今回の記事は入門 統計的因果推論 の３章の部分の数式の変形等、ぱっと読んで分かりづらくて時間をかけて考えてしまった点を中心にあとから自分で見返してわかるように数式の変形を説明した記事になります。

前提として「入門 統計的因果推論」で事前に説明された用語に関して、わかりやすくて説明が不要な部分は説明せずに使っているので、この記事だけではおそらく内容がわからない部分もあるかもしれませんがご了承ください。

調整化公式の導出 (3.2 調整)

まず、新薬の効果を表す問題を考えます。考える因果グラフは以下の通り。

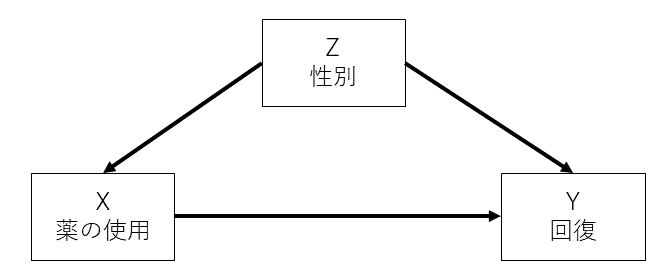
この問題において以下の平均因果効果（ACE: average causal effect）が知りたいことです。

$$ \begin{align*}
ACE=P(Y = 1 | do(X = 1)) – P(Y = 1 | do(X = 0))
\end{align*} $$

この式から\( P(Y| do(X)) \) の確率を観測データから計算できればACEの計算ができることがわかります。このため、これ以降は\( P(Y| do(X)) \)を観測データから計算する方法について説明していきます。具体的には以下の形に変形することを目指します。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z P(Y|X, Z=z)P(Z=z) \\
\tag{3.1}
\end{align*} $$

この式が調整化公式と呼ばれるものです。

ここで、\( do()\) はdo演算子といいます。これは変数\(X\) が自然に値\(x\)をとる場合と \( X=x \) に固定する場合を区別して表記したいという理由から、値を固定する後者の場合を\( do(X=x) \) と表記するために用いています。例示した図3.1の因果グラフにおいては、\(Z\)に依存した何等かの理由により薬を使った人のうち回復する確率を \( P(Y = 1 | X = 1) \) 、\(Z\)によらず、全員に対して薬を使うように固定した場合の回復する確率を \( P(Y = 1 | do(X = 1)) \)と表しています。固定して薬を使うようなケースは介入試験で全員に薬を使った場合などを指します。

言葉だとわかりづらいと思うので因果グラフでも示します。\(do(X=x)\) というように\(X \) を固定した場合の修正後の因果グラフは以下のようになります。

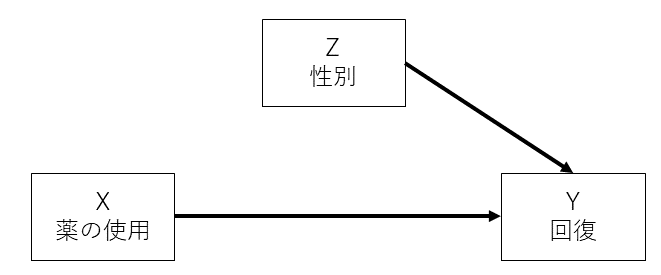
この因果グラフにおける確率を本にならって\(P_m\) と表記します。この修正後の因果グラフの確率\(P_m\)を利用すると\( P(Y | do(X)) \) は以下のように表すことができます。

$$ \begin{align*}
P(Y | do(X)) = P_m(Y|X) \tag{3.2} \\
\end{align*} $$

この後はこの\(P(Y | do(X)) \)が式変形により\(P_m\)に依存しない形に式変形できることを示します。これができると介入試験のデータを使わずに観察データから\(P(Y | do(X)) \)が求められることとになります。

\(P(Y | do(X)) \)の式変形の前に後ほど式変形で重要な関係を以下に列挙しておきます。

$$ \begin{align*}
P_m(Z) =& P(Z) \tag{3.3} \\
P_m(Y|X, Z) =& P(Y|X, Z) \tag{3.4} \\
\end{align*} $$

式(3.3)は\(Z\) が\(X\)の介入による影響がないため、式(3.4)は\(X\)と\(Z\)が条件付けされた状況下において、\(Y\)の確率は修正前後で変化しないため成り立ちます。

それでは\(P(Y | do(X)) \)の式変形をしていきます。まず、先ほど示した通り、以下のように\(P_m\)を利用すると以下のように表すことができます。

$$ \begin{align*}
P(Y | do(X)) = P_m(Y|X) \tag{3.2} \\
\end{align*} $$

ここで、確率の周辺化が以下のような式で行えることを利用します。

$$ \begin{align*}
P(Y) =& \sum_x P(Y, X=x) \tag{3.5} \\
\end{align*} $$

この周辺化の式を利用して式(3.2)を\(P_m(Y, Z|X) \)の同時確率の式で書きます。

$$ \begin{align*}
P(Y | do(X)) &= P_m(Y|X) \\
&= \sum_z P_m(Y, Z=z | X) \tag{3.6}
\end{align*} $$

次に\(P_m(Y, Z | X)\)の部分を条件付き確率の定義を利用します。条件付き確率の定義より\( P_m(Y|X, Z) \)の部分は以下のようになります。

$$ \begin{align*}
P_m(Y|X, Z) &= \frac{P_m(Y, Z | X)}{P_m(Z|X)} \tag{3.7}
\end{align*} $$

後ほどの説明で分かりやすいように式(3.7)の左右を入れ替えて、両辺を\(P_m(Z|X)\)でかけると以下の式になります。

$$ \begin{align*}
\frac{P_m(Y, Z | X)}{P_m(Z|X)} &= P_m(Y|X, Z) \\
\frac{P_m(Y, Z | X)P_m(Z|X)}{P_m(Z|X)} &= P_m(Y|X, Z)P_m(Z|X) \\
P_m(Y, Z | X) &= P_m(Y|X, Z)P_m(Z|X) \tag{3.8}
\end{align*} $$

ここで修正後の因果グラフにおいて\(Z\)は\(X\)と独立なことを利用すると以下のように変形できます。

$$ \begin{align*}
P_m(Z|X) = P_m(Z) \tag{3.9}
\end{align*} $$

式(3.3)、 (3.4)、(3.9) を利用すると式(3.8)は以下のように変形できます。

$$ \begin{align*}
P_m(Y, Z | X) &= P_m(Y|X, Z)P_m(Z|X) \\
&= P_m(Y|X, Z)P_m(Z) \\
&= P_m(Y|X, Z)P(Z) \\
&= P(Y|X, Z)P(Z) \\
\tag{3.10}
\end{align*} $$

この式(3.10)を式(3.6)に代入すると以下のようになります。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z P_m(Y, Z=z | X) \\
&= \sum_z P(Y|X, Z=z)P(Z=z) \\
\tag{3.11}
\end{align*} $$

以上の結果から式(3.1)を導出できました。

調整化公式を傾向スコアを使った形に変形する (3.2.1 調整すべきか否か)

先ほど示した調整化公式を因果推論でよく使われる傾向スコアを使った以下の形の式に変形します。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z \frac{P(X, Y, Z=z)}{P(X|Z=z)} \\
\tag{3.12}
\end{align*} $$

ここで\(P(Z|X)\)が傾向スコアです。

では、調整化公式の式(3.1)を式(3.12)の形を目指して変形していきます。まずは右辺の\(P(Y|X, Z=z)P(Z=z)\)に注目します。ここで、\(P(X|Z)/P(X|Z)\)をかけます。

$$ \begin{align*}
P(Y|X, Z)P(Z) &= \frac{P(Y|X, Z)P(X|Z)P(Z)}{P(X|Z)} \\
\tag{3.13}
\end{align*} $$

ここで分子の部分について条件付き確率の定義から\(X\)と\(Z\)を条件付けせずに同時確率の形で書くことができます。具体的には以下のように変形できます。

$$ \begin{align*}
P(Y|X, Z)P(X|Z)P(Z) &= P(X, Y|Z)P(Z) \\
&= P(X, Y, Z) \\
\tag{3.14}
\end{align*} $$

この式(3.13)、(3.14)を利用すると式(3.11)は以下のように変形できます。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z P(Y|X, Z=z)P(Z=z) \\
&= \sum_z \frac{P(Y|X, Z=z)P(X|Z=z)P(Z=z)}{P(X|Z=z)} \\
&= \sum_z \frac{P(X, Y, Z=z)}{P(X|Z=z)} \\
\tag{3.15}
\end{align*} $$

これで求めたかった式(3.12)を導出することができました。

フロントドア公式の導出 (3.4 フロントドア基準)

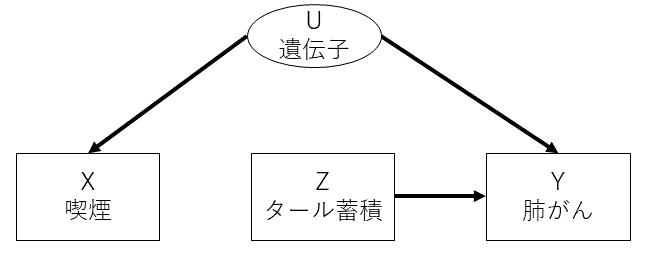
次にフロントドア公式の導出について説明していきます。ここでは以下の因果グラフを考えます。

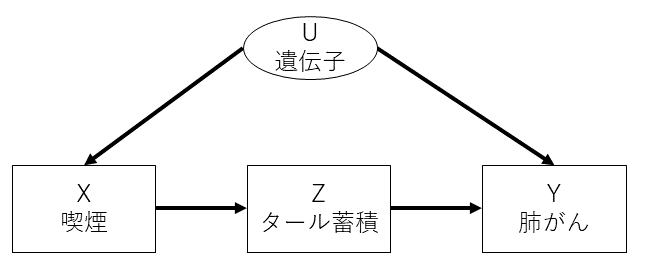
\(U\)は観測されていない交絡因子なので、この\(U\)を使わない形で\(X\)の効果、ここでは喫煙の肺がんへの影響があるかを考えます。これを考えるうえで、変数\(Z\)、ここではタール蓄積が観測できているとします。そして、ゴールとして因果効果を測るうえで、\(P(Y|do(X))\) という確率が求められれば良いと考えます。

本のほうの説明ではバックドア基準を２度にわたって適用すればよいと書かれています。しかし、この意味がなんとなくでしか私は理解できなかったので、私なりに\(P(Y|do(X))\)を式変形していってフロントドア公式を導出していきます。具体的には先ほどの因果グラフにおいて以下の式の導出を行います。

$$ \begin{align*}
P(Y | do(X=x)) &= \sum_z P(Y|do(Z=z))P(Z=z | do(X=x)) \\
&= \sum_z \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z=z)P(Z=z | X=x) \tag{3.16}
\end{align*} $$

ではフロンドドア公式の導出を始めます。まずは式(3.16)の１行目のdo演算子を使った式を目指して\(P(Y|do(X))\)を変形していきます。まず、\(P(Y|do(X))\)を周辺化の式(3.6)を利用して\(P(Y, Z|do(X))\)という同時確率を使った式に変形し、その後、\(Z\)で条件付けした確率に変形させます。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z P(Y, Z=z|do(X)) \\
&= \sum_z P(Y|do(X), Z=z)P(Z=z | do(X)) \tag{3.17}
\end{align*} $$

ここで、因果グラフより\(X\)から\(Y\)につながるパスは\(X \rightarrow Z \rightarrow Y \)しかありません。このため、\(Z\)で条件付けされていると変数\(Y\)は\(X\)とは独立となっています。このため、\(P(Y|do(X), Z=z)\)の部分は以下のようになります。

$$ \begin{align*}
P(Y|do(X), Z) &= P(Y|Z) \tag{3.18}
\end{align*} $$

次に、周辺化の式を利用して\(P(Y|Z)\)を\(X\)を加えた同時確率で表現したあと、\(X\)の条件付き確率の形を使って表します。

$$ \begin{align*}
P(Y|Z) &= \sum_{x^{\prime}} P(X=x^{\prime}, Y|Z) \\
&= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime}) \tag{3.18}
\end{align*} $$

次に\(P(Y|X, Z)\)を変形していきます。ただ、ここからだと分かりにくいので\(P(Y|do(Z))\)から式変形していって、\(P(Y|X, Z)\)になることを示します。基本の流れは調整化公式の導出と同じ流れです。

まず、わかりやすいように\(do(Z)\)で修正された因果グラフを示します。

この因果グラフにおける確率を\(P_{z}\) とすると\(P(Y|do(Z))\)を\(P_{z}\)で表したあと、確率の周辺化と条件付きの定義を利用して変形していくと以下の通りです。

$$ \begin{align*}
P(Y|do(Z)) &= P_z(Y|Z) \\
&= \sum_{x^{\prime}} P_z(Y, X=x^{\prime}|Z) \\
&= \sum_{x^{\prime}} P_z(Y|X=x^{\prime}, Z)P_z(X=x^{\prime}|Z) \tag{3.19}
\end{align*} $$

また、修正前後の因果グラフより以下が成り立ちます。

$$ \begin{align*}
P_z(X|Z) &= P_z(X) \tag{3.20} \\
P_z(X) &= P(X) \tag{3.21} \\
P_z(Y|X, Z) &= P(Y|X, Z) \tag{3.22} \\
\end{align*} $$

この式(3.20)から(3.22)を利用して式(3.19)の\(P_z(Y|X, Z)P_z(X|Z) \)の部分を以下のように変形します。

$$ \begin{align*}
P_z(Y|X, Z)P_z(X|Z) &= P_z(Y|X, Z)P_z(X) \\
&= P_z(Y|X, Z)P(X) \\
&= P(Y|X, Z)P(X) \tag{3.23}
\end{align*} $$

この式(3.23)を利用すると式(3.19)は以下のようになります。

$$ \begin{align*}
P(Y|do(Z)) &= \sum_{x^{\prime}} P_z(Y|X=x^{\prime}, Z)P_z(X=x^{\prime}|Z) \\
&= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime})
\tag{3.24}
\end{align*} $$

この式(3.24)と式(3.19)を利用すると式(3.18)は以下のようになります。

$$ \begin{align*}
P(Y|do(X), Z) &= P(Y|Z) \\
&= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime}) \\
&= P(Y|do(Z)) \tag{3.25}
\end{align*} $$

よって式(3.25)を利用して式(3.17)を変形するとまず求めたかった式(3.16)のdo演算子を使った形になります。

$$ \begin{align*}
P(Y | do(X)) &= \sum_z P(Y|do(X), Z=z)P(Z=z | do(X)) \\
&= \sum_z P(Y|do(Z=z))P(Z=z | do(X)) \tag{3.26}
\end{align*} $$

ここまでで、式(3.16)の1行目のdo演算子を使った式ができました。ここから、do演算子のない形に変形していきます。

まず、式(3.24)の式を使い\(do(Z)\)を使わない形に式(3.26)を変形します。ここから\(X\)の値が2種類でてくるので区別できるように\(x\)と\(x^{\prime}\)の二つに分けます。

$$ \begin{align*}
P(Y | do(X=x)) &= \sum_z P(Y|do(Z=z))P(Z=z | do(X=x)) \\
&= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime})P(Z=z | do(X=x)) \\
\tag{3.27}
\end{align*} $$

次に\(P(Z=z | do(X=x))\)の部分で\(do(X)\)がない形に変形することを目指します。ここで元の因果グラフを見ると\(X\) から\(Z\)につながるパスは\(X \rightarrow Z \)しかないため、因果グラフから以下の等式が成り立ちます。

$$ \begin{align*}
P(Z| do(X)) &= P(Z|X)
\tag{3.28}
\end{align*} $$

（\(do(X)\)によって修正された因果グラフを考えて\(P(Z=z | do(X=x))\)を修正後の因果グラフの確率から観測データから計算できる確率にするにはどうすればよいのか考えてもいいのですが、自明なので省略します。）

この式(3.28)を利用すると式(3.27)は以下のように変形できます。

$$ \begin{align*}
P(Y | do(X=x)) &= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime})P(Z=z | do(X=x)) \\
&= \sum_{x^{\prime}} P(Y|X=x^{\prime}, Z)P(X=x^{\prime})P(Z=z | X=x) \tag{3.29}
\end{align*} $$

この式は求めたかった式（3.16）の式になっています。これでフロントドア公式を導出することができました。

終わりに

今回の記事では入門 統計的因果推論 の３章の部分で私がぱっとわからなかった部分の式変形を中心に説明する記事を書きました。本当はCDE (Controlled direct effect) (本で3.7 媒介で説明されていた部分)もぱっとわからなかったのですが、ここに関しては４章の内容とまとめて説明したほうが分かりやすいので、４章の記事のときに説明しようと思います。

この記事がこの本を読む他の人にも役に立てば幸いです。